Sure, DeepMind’s AI is impressive, but can it guide human intuition?

This article is part of our reviews of AI research papers, a series of posts that explore the latest findings in artificial intelligence.

Deep learning can help discover mathematical relations that evade human scientists, a recent paper by researchers at DeepMind shows. Like many things coming from the Alphabet-owned artificial intelligence lab, the paper, which is titled “Advancing mathematics by guiding human intuition with AI,” has received much attention from science and tech media.

Some mathematicians and computer scientists have lauded DeepMind’s efforts and the findings in the paper as breakthroughs. Others are more skeptical and believe that the use of deep learning in mathematics might have been overstated in the paper and its coverage in popular press.

The results are nonetheless fascinating and can expand the toolbox of scientists in discovering and proving mathematical theorems.

A framework for mathematical discovery with machine learning

The 💜 of EU tech

The latest rumblings from the EU tech scene, a story from our wise ol' founder Boris, and some questionable AI art. It's free, every week, in your inbox. Sign up now!

In their paper, the scientists at DeepMind suggest that AI can be used to “assist in the discovery of theorems and conjectures at the forefront of mathematical research.” They propose a “framework for augmenting the standard mathematician’s toolkit with powerful pattern recognition and interpretation methods from machine learning.”

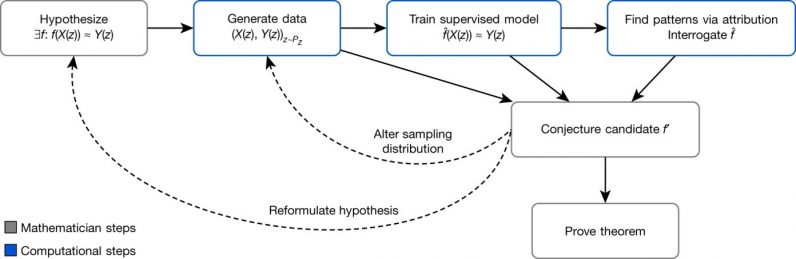
Mathematicians start by making a hypothesis about the relation between two mathematical objects. To verify the hypothesis, they use computer programs to generate data for both types of objects. Next, a supervised machine learning model algorithm crunches the numbers and tries to tune its parameters that map one type of object to the other.

“The key contributions of machine learning in this regression process are the broad set of possible nonlinear functions that can be learned given a sufficient amount of data,” the researchers write.

If the trained model performs better than random guessing, then it might indicate that there is indeed a discoverable relation between the two mathematical objects. Using various machine learning techniques, the researchers can find the data points that are more relevant to the problem, reform their hypothesis, generate new data, and train new models. By repeating these steps, they can narrow down the set of plausible conjectures and speed their way toward a final solution.

DeepMind’s scientists describe the framework as a “test bed for intuition” that can quickly verify “whether an intuition about the relationship between two quantities may be worth pursuing” and provide guidance as to how they may be related.

Using this framework, the DeepMind researchers used deep learning to reach “two fundamental new discoveries, one in topology and another in representation theory.”

An interesting aspect of the work was that it did not require the huge amount of compute power that has become a mainstay of DeepMind’s research. According to the paper, the deep learning models used in both discoveries can be trained “within several hours on a machine with a single graphics processing unit.”

Knots and representations

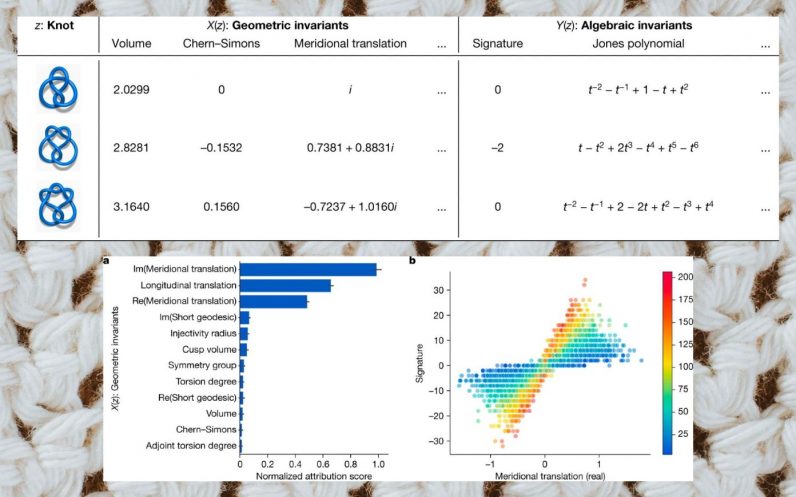
Knots are closed loops in dimensional space that can be defined in various ways. They become more complex as the number of their crossings grows. The researchers wanted to see whether they could use machine learning to discover a mapping between algebraic invariants and hyperbolic invariants, two fundamentally different ways of defining knots.

“Our hypothesis was that there exists an undiscovered relationship between the hyperbolic and algebraic invariants of a knot,” the researchers write.

Using the SnapPy software package, the researchers generated the “signature,” an algebraic invariant, and 12 promising hyperbolic invariants for 1.7 million knots with up to 16 crossings.

Next, they created a fully connected, feed-forward neural network with three hidden layers, each having 300 units. They trained the deep learning model to map the values of the hyperbolic invariants to the signature. Their initial model was able to predict the signature with 78 percent accuracy. Further analysis brought them to a smaller set of parameters in the hyperbolic invariants that were predictive of the signature. The researchers refined their conjecture, generated new data, retrained their models, and reached a final theorem.

The researchers describe the theorem as “one of the first results that connect the algebraic and geometric invariants of knots and has various interesting applications.”

“We expect that this newly discovered relationship between natural slope and signature will have many other applications in low-dimensional topology. It is surprising that a simple yet profound connection such as this has been overlooked in an area that has been extensively studied,” the researchers write.

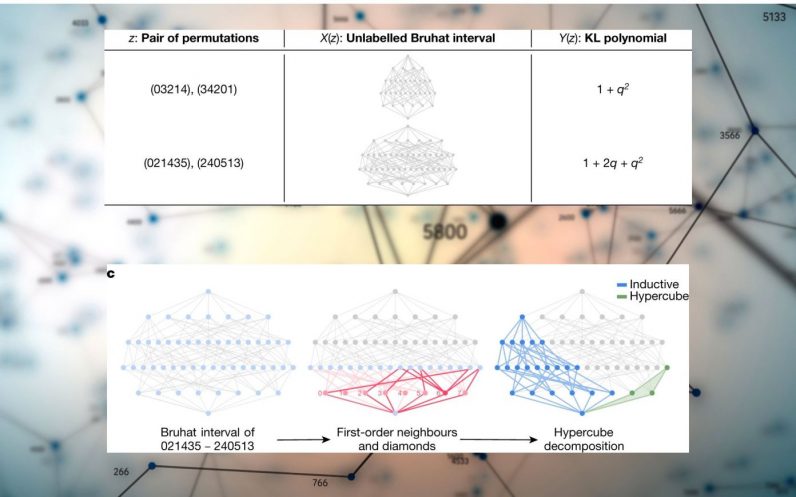
The second result in the paper is also a mapping of two different views of symmetries, a problem that is much more complicated than knots.

In this case, they used a type of graph neural network (GNN) to find relations between Bruhat interval graph and the Kazhdan-Lusztig (KL) polynomial. One of the benefits of GNNs is that they can compute and learn graphs that are very large and hard to manage for the unaided mind. The deep learning model takes the interval graph as input and tries to predict the corresponding KL polynomial.

Again, by generating data, training DL models, and readjusting the process, the scientists were able to formulate a provable conjecture.

Reactions to DeepMind’s math AI

Speaking about DeepMind’s discovery in knot theory, Mark Brittenham, a knot theorist at the University of Nebraska–Lincoln told Nature, “The fact that the authors have proven that these invariants are related, and in a remarkably direct way, shows us that there is something very fundamental that we in the field have yet to fully understand.” Brittenham added that, in comparison to other efforts to apply machine learning to knots, DeepMind’s technique is novel in its ability to discover surprising connections.

Adam Zsolt Wagner, a mathematician at Tel Aviv University, Israel, who also spoke to Nature, said that the methods presented by DeepMind could prove valuable for certain kinds of problems.

Wagner, who has experience in applying machine learning to mathematics, said, “Without this tool, the mathematician might waste weeks or months trying to prove a formula or theorem that would ultimately turn out to be false.” But he also added that it is unclear how broad its impact will be.

Reasons to be skeptical

Following the publication of DeepMind’s work in Nature, Ernest Davis, Computer Science Professor at New York University, published a paper of his own, which raises some important questions about DeepMind’s framing of the results and the limits of applying deep learning to mathematics in general.

On the first result presented in DeepMind’s paper, Davis observes that knot theory is not the kind of problem where deep learning typically outshines other machine learning or statistical methods.

“DL’s strength is in cases like vision or text where each instance (image or text) has a large number of low-level input features, it is hard to reliably identify high-level features, and the function relating the input features to the answer is, as far as anyone can tell, immensely complex, with no small subset of the input features being at all determinative,” Davis writes.

The knot problem had only twelve input features, of which only three turned out to be relevant. And the mathematical relation between the input features and target variable was simple.

“It is hard to see why a neural network with 200,000 parameters would be the method of choice; simple, conventional statistical methods or a support vector machine would be more suitable,” Davis writes.

In the second project, the role of deep learning was much more relevant, Davis notes. “Unlike the knot theory project, which used a generic DL architecture, the neural network was carefully designed to fit deep mathematical knowledge about the problem. Moreover, the DL worked much better, with something like 1/40th the error rate, on pre-processed data than on the original data,” he writes.

On the one hand, the results cut against criticism pertaining that it is hard to incorporate domain knowledge into deep learning, Davis notes. “On the other hand, enthusiasts for DL have often praised DL as a ‘plug-and-play’ learning methodology that can be thrown at raw data for whatever problem comes to hand; this cuts against that praise,” he writes.

Davis also notes that the success of applying deep learning to these tasks may depend critically on the way the training data is generated and the way that the mathematical structures are encoded. This suggests that the framework might be applicable to a narrow class of mathematical problems.

“Finding the best way to generate and encode data involves a mixture of theory, experience, art, and experimentation. The burden of all this lies on the human expert,” he writes. “Deep learning can be a powerful tool, but it is not always a robust one.”

Davis warns that in the current climate of hype surrounding deep learning, “there is a perverse incentive to focus the role of the DL in this research, not just for the ML specialists from DeepMind, but even for the mathematicians.”

Davis concludes that, as used in the paper, deep learning is best viewed as “another analytic tool in the toolbox of experimental mathematics rather than as a fundamentally new approach to mathematics.”

It is worth noting that the authors of the original paper have also pointed out some of the limits of their framework, including that “it requires the ability to generate large datasets of the representations of objects and for the patterns to be detectable in examples that are calculable. Further, in some domains the functions of interest may be difficult to learn in this paradigm.”

Deep learning and intuition

One of the topics of controversy is the paper’s claim that deep learning is “guiding intuition.” Davis describes this claim as a “seriously inaccurate description of the assistance that mathematicians have gained, or can hope to gain, from this use of DL systems.”

Intuition is one of the key differentiators between human and artificial intelligence. It is the ability to make decisions that are better than random guesses and can direct you in the right direction most of the time. As the history of AI has so far shown, intuition is not captured in countless predefined rules or patterns found in vast amounts of data.

“In the mathematical setting, the word ‘intuitive’ means that a concept or a proof can be grounded in a person’s deep-seated sense of familiar domains such as numerosity, space, time, or motion, or in some other way ‘makes sense’ or ‘seems right’ in a way that does not involve explicit calculation or step-by-step reasoning,” Davis writes.

While obtaining an intuitive grasp of mathematical concepts often requires working through multiple specific examples, it is not a work of statistical correlations, Davis argues. In other words, you don’t gain intuitions by running millions of examples and observing the percent of times certain patterns recur.

This means that it was not the deep learning models that provided the scientists with an intuitive understanding of the concepts they defined, the theorems they proved, and the conjectures they put forward.

Writes Davis, “What the DL did was to give them some advice as to which features of the problem seemed to be important and which seemed unimportant. That is not to be sneezed at, but it should not be exaggerated.”

This article was originally published by Ben Dickson on TechTalks, a publication that examines trends in technology, how they affect the way we live and do business, and the problems they solve. But we also discuss the evil side of technology, the darker implications of new tech, and what we need to look out for. You can read the original article here.